并查集主要用于处理一些不相交集合的问题。
每个集合包含一个或多个元素,并且有一个代表元素。对于给定一个元素,可以快速找到其所属集合的代表元素,这样判断两个元素是否属于同一集合,只需要判断二者所属集合的代表元素是否一致即可。
如果要合并两个集合,只需要将其中一个集合的代表元素设为另一个集合的代表元素即可。
即,并查集主要应用于两个操作:
- 将两个集合合并
- 查询两个元素是否属于同一个集合
涉及到的主要操作有两个
- 合并:把两个元素所属集合合并(前提是两个集合不相交)
void join(int a, int b)
{
int tmpa,tmpb;
tmpa = find_root(a);
tmpb = find_root(b);
if(tmpa!=tmpb)
root[tmpa] = tmpb;
}
- 查找根(代表元素):找到某一个元素的所属集合的根。
int find_root(int x)
{
while(x!=root[x])
x = root[x];
return x;
}
//root[x]=y表示x的根是y,初始化时,每个元素的根都是自己
路径压缩*
查找根最坏的一种情况是一条常常的链,这时候查找的效率会大大降低,此时可以使用路径压缩,即将每个元素直接指向根节点 ,如下图。
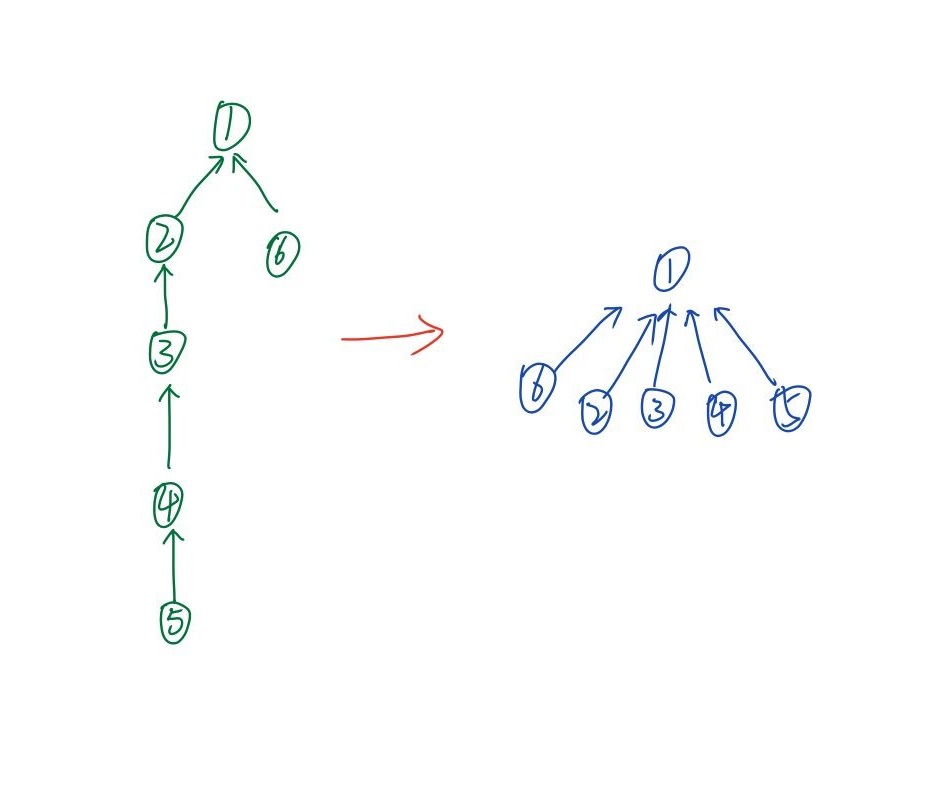
我们可以在查找的过程中把每个元素的父节点直接设成根节点。
int find_root(int x)
{
int root_of_x = x; //根节点
// 找到x的根节点
while(root_of_x != root[root_of_x])
root_of_x = root[root_of_x];
//将x到root_of_x路径上的每个节点的父节点都换成根节点x的根节点
while(x != root[x])
{
int tmp = x;
x = root[x];
root[tmp] = root_of_x;
}
return root_of_x;
}