【数据结构】二叉树

二叉树的存储

1. 顺序存储结构

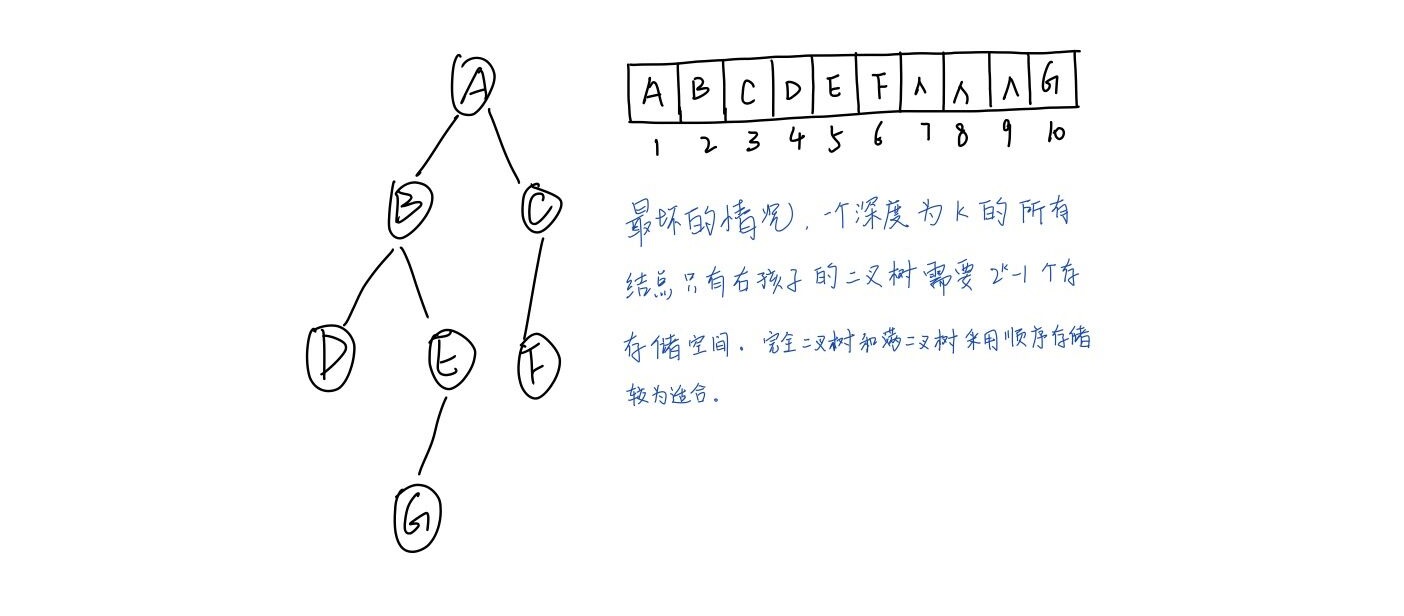
2.链式存储

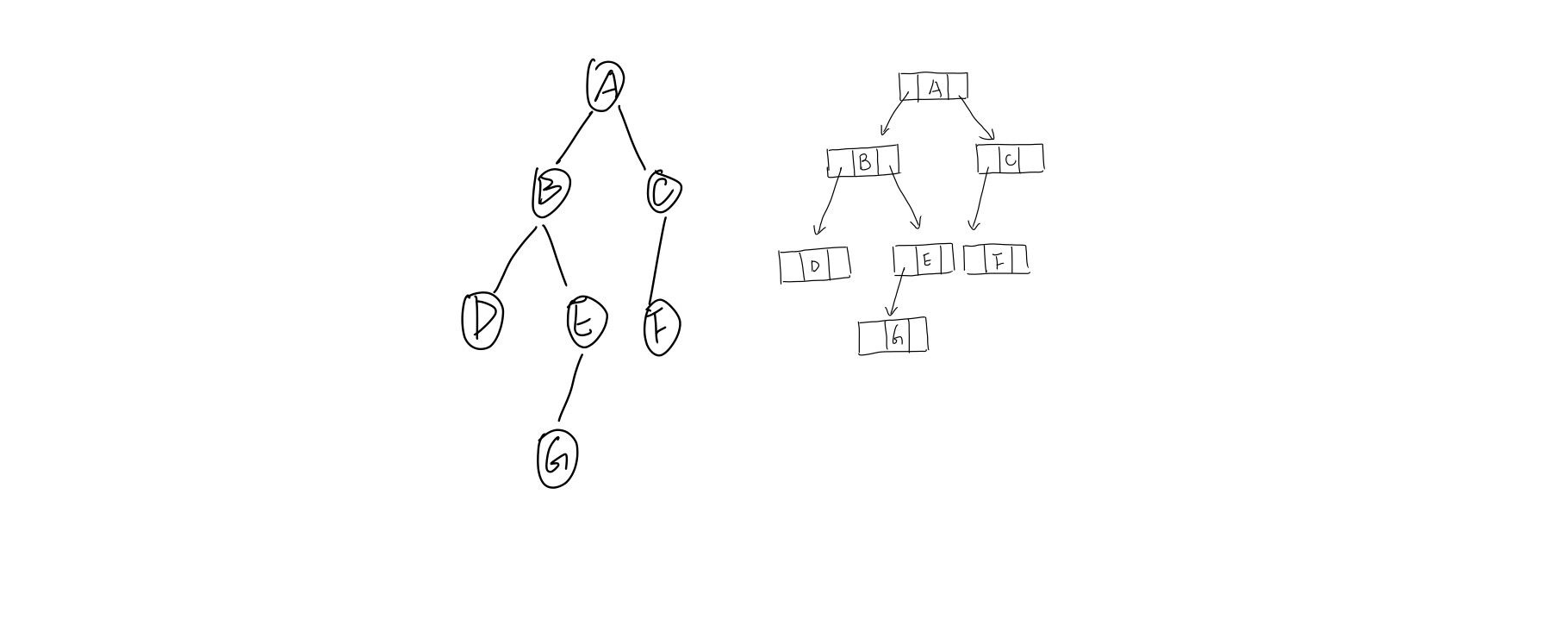
typedef struct node
{
    int data;
    struct node *lchild, *rchild;
}Bitree;

二叉树的访问

先序访问

void preOrderTraveral(Bitree *node) //递归
{
    if(node == NULL)
    {
        return;
    }
    printf("%d ",node->data);
    preOrderTraveral(node->lchild);
    preOrderTraveral(node->rchild);
}


void _preOrderTraveral(Bitree *node) //非递归
{
    stack<Bitree*> s;
    Bitree *tmp_node = node;
    while(tmp_node!=NULL || !s.empty())
    {
        while(tmp_node != NULL)
        {
            printf("%d ",tmp_node->data);
            s.push(tmp_node);
            tmp_node = tmp_node->lchild;
        }
        if(!s.empty())
        {
            tmp_node = s.top();
            s.pop();
            tmp_node = tmp_node->rchild;
        }
    }
}

中序访问

void inOrderTraveral(Bitree *node)
{
    if(node == NULL)
    {
        return;
    }
    inOrderTraveral(node->lchild);
    printf("%d ",node->data);
    inOrderTraveral(node->rchild);
}


void _inOrderTraveral(Bitree *node)
{
    stack<Bitree*> s;
    Bitree *tmp_node = node;
    while(tmp_node!=NULL || !s.empty())
    {
        while(tmp_node != NULL)
        {
            s.push(tmp_node);
            tmp_node = tmp_node->lchild;
        }
        if(!s.empty())
        {
            tmp_node = s.top();
            s.pop();
            printf("%d ",tmp_node->data);
            tmp_node = tmp_node->rchild;
        }
    }
}

后序访问

void postOrderTraveral(Bitree *node)
{
    if(node == NULL)
    {
        return;
    }
    postOrderTraveral(node->lchild);
    postOrderTraveral(node->rchild);
    printf("%d ",node->data);
}


void _postOrderTraveral(Bitree *node)
{
    stack<Bitree*> s;
    Bitree *tmp_node = node, *lastVisit = NULL;
    while(tmp_node!=NULL || !s.empty())
    {
        while(tmp_node != NULL) //左节点入栈
        {
            s.push(tmp_node);
            tmp_node = tmp_node->lchild;
        }
        if(!s.empty())
        {
            tmp_node = s.top();
            s.pop();
            if(tmp_node->rchild==NULL || tmp_node->rchild==lastVisit) //此节点右孩子为空或者已访问过，那么访问此节点
            {
                printf("%d ",tmp_node->data);
                lastVisit = tmp_node;
                tmp_node = NULL;
            }
            else
            {
                s.push(tmp_node);//如果有右孩子并且每访问过，再将此结点入栈
                tmp_node = tmp_node->rchild;
            }
        }
    }
}

层次遍历
二叉树的层次遍历基于广度优先搜索，在访问第n层时，一定会访问完第n-1层。

void levelOrder(Bitree *root)
{
    if(!root) return;
    queue<Bitree *> q;
    q.push(root);
    while(!q.empty())
    {
        Bitree tmp = q.front();
        q.pop();
        printf("%d",tmp->data);
        if(tmp->lchild) q.push(tmp.lchild);
        if(tmp->rchild) q.push(tmp.rchild);
    }
}

0二叉搜索树

左子树的所有结点值均小于根结点的值；右子树的所有结点值均大于根结点的值；左子树也是二叉搜索树。

二叉搜索树的构建

typedef struct TreeNode
{
    int val;
    struct TreeNode *lchild, *rchild;
}TreeNode;

void Create(TreeNode *root, int tmp)
{
    if(!root)
    {
        root = (TreeNode *)malloc(sizeof(TreeNode));
        root->val = tmp;
        return;
    }
    if(root->val < tmp)
        Create(root->lchild,tmp);
    else
        Create(root->rchild,tmp);
}

二叉搜索树结点的删除

如果删除的结点只有左孩子或者只有有孩子，那么直接删除，然后把其孩子加到父节点上。
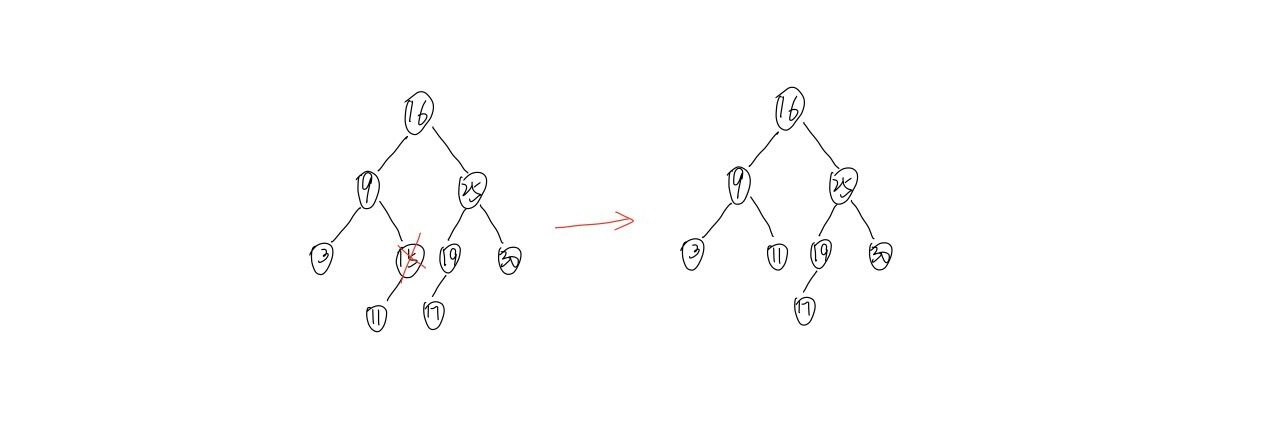
如果删除的结点有左孩子和有孩子，那么删除此节点后，需要将其左子树的最大结点或者右子树的最小节点替换上来。

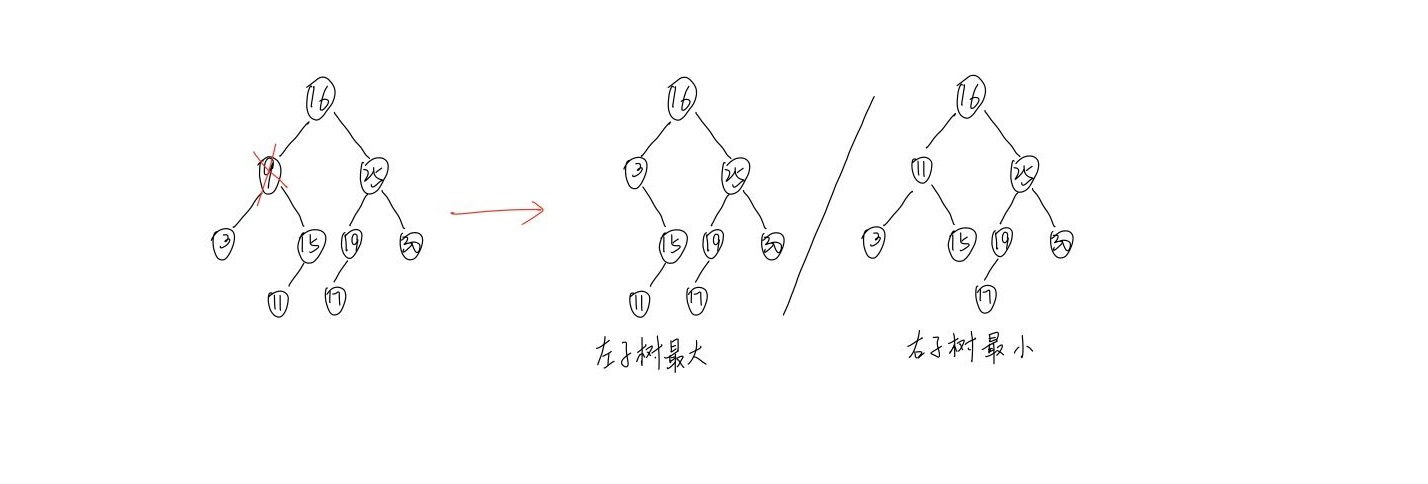
找到二叉搜索树两个结点的最近的双亲结点

利用二叉搜索树的特点，遍历整个二叉树，如果两个节点都小于当前遍历结点，那么递归到其左子树；如果两个结点都大于当前遍历结点，那么递归到其右子树上，如果一个大于一个小于当前遍历结点，那么此结点即为其最近的双亲结点。

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    if(root->val > p->val && root->val > q->val)
        return lowestCommonAncestor(root->left,p,q);
    else if (root->val < p->val && root->val < q->val)
        return lowestCommonAncestor(root->right,p,q);
    return root;
}

二叉搜索树的中序遍历是递增顺序

由中序和后序还原二叉树

后序中右起第一位3肯定是根结点，我们可以据此找到中序中根结点的位置rootin；
中序中根结点左边就是左子树结点，右边就是右子树结点，即[左子树结点，根结点，右子树结点]，我们就可以得出左子树结点个数为int left_count = tmp - inleft;；
后序中结点分布应该是：[左子树结点，右子树结点，根结点]；
根据前一步确定的左子树个数，可以确定后序中左子树结点和右子树结点的范围；
如果我们要前序遍历生成二叉树的话，下一层递归应该是：

左子树：root->left = pre_order(中序左子树范围，后序左子树范围，中序序列，后序序列);；
右子树：root->right = pre_order(中序右子树范围，后序右子树范围，中序序列，后序序列);。

每一层递归都要返回当前根结点root；

TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
    TreeNode *root = pre_order(0,inorder.size()-1, 0,postorder.size()-1, inorder, postorder);
    return root;
}

TreeNode *pre_order(int inleft, int inright, int postleft, int postright, vector<int> &inorder, vector<int>& postorder)
{
    if(inleft>inright) return NULL;
    TreeNode *root = new TreeNode(postorder[postright]);
    int tmp = inleft;
    while(inorder[tmp]!=postorder[postright]) tmp++;
    int left_count = tmp - inleft; //左子树的结点个数
    root->left = pre_order(inleft,tmp-1,postleft,postleft+left_count-1,inorder,postorder);
    root->right = pre_order(tmp+1,inright,postleft+left_count,postright-1,inorder,postorder);
    return root;
}