【算法】数学

质数

线性筛选质数：

出现一个数，则把已这个数为因子的数都标记为合数。

• 如2，所以4,6,8 10....都标记为合数
• 如3，所以9,12,15.....都标记为合数
• 如4，所以16,20,24...都标记为合数

即，若i是素数，则从 j=i*i 开始，把 j+i , j+2i , j+3i .....都标记为合数 （因为2*i, 3*i, 4*i, ...., (i-1)*i 分别是2, 3, 4, ..., i-1的倍数，已经在i之前标记过，所以从j=i*i开始标记）

筛法的思想是去除要求范围内所有的合数，剩下的就是素数了，而任何合数都可以表示为素数的乘积，因此如果已知一个数为素数，则它的倍数都为合数。

const int N = 1e5;
int prime[N] = {0};
for(int i = 2; i <= sqrt(N + 1); i++)
{
    if(!prime[i])
    {
        for(int j = i + 1; j <= N; j += i)
            prime[j] = 1;
    }
}

分解质因数

void primeFactor(int n)
{
    int x = sqrt(n) + 1;
    for(int i=2; i<x; i++)
    {
        int cnt = 0; // cnt表示该质因数的幂次
        while(n % i == 0) //输出所有可以约去的数
        {
            cnt ++;
            n /= i;
        }
        if(cnt) cout << i << " " << cnt << endl;
    }
    if(x > 1) cout << x << " " << 1 << endl;
}

一个自然数的约数个数是它各质因数的次数分别加1相乘的积。
例：18的因数有：1，2，3，6，9，18。而其质因数有18=2×2×3。

即(1+1) * (2+1)=6个。

欧拉函数

https://www.acwing.com/problem/content/875/

欧拉函数的定义：1~N中与N互质的数的个数被称为欧拉函数，记为φ(n)

$一个数的质因数N = p^{a_{1}}_{1}p^{a_{2}}_{2}...p^{a_{m}}_{m}$

则一个数的欧拉函数的定义：

$\phi(N) = N * \frac{p_{1}-1}{p_{1}} * \frac{p_{2}-1}{p_{2}} * ... * \frac{p_{m}-1}{p_{m}}$

package main

import "fmt"

func main() {
    var n int
    
    fmt.Scanf("%d", &n)
    
    for i := 0; i < n; i++ {
        hash := make(map[int]int)
        var tmp int
        fmt.Scanf("%d", &tmp)
        var ans int = tmp
        for j := 2; j <= tmp / j; j++ {
            for tmp % j == 0 {
                tmp /= j
                hash[j] ++
            }
        }
        if tmp > 1 {
            hash[tmp] ++
        }
        
        for k, _ := range hash {
            ans = ans / k * (k - 1)
        }
        
        fmt.Println(ans)
        
    }
}

约数

求一个数的约数的个数

求一个数n的约数，可以直接遍历1~n，看能不能整除n即可。

求一个很大的数的约束的个数：

$分解质因数：n = p_{0}^{a_{0}}*p_{2}^{a_{1}}*...*p_{n}^{a_{n}}$

$其中p_{0}^{a_{0}}的约数为：1,p_{0},p_{0}^{2},...,p_{0}^{a_{0}}共a_{0}+1个$

$因此n的约束的个数：(a_{0}+1)*(a_{1}+1)*...*(a_{n}+1)$

https://www.acwing.com/problem/content/description/872/

package main

import "fmt"

func main() {
    var n int
    hash := make(map[int]int)
    fmt.Scanf("%d", &n)
    
    for i := 0; i < n; i++ {
        var tmp int
        fmt.Scanf("%d", &tmp)
        n := tmp
        for j := 2; j <= n / j; j++ {
            for tmp % j == 0 {
                tmp /= j
                hash[j]++
            }
        }
        if tmp > 1 {
            hash[tmp] ++
        }
    }
    var ans int = 1
    for _, v := range hash {
        ans = (ans * (v + 1) ) % (1e9 + 7)
    }
    fmt.Printf("%d\n", ans)
    
}

模运算

字符串哈希

https://leetcode-cn.com/problems/find-substring-with-given-hash-value/

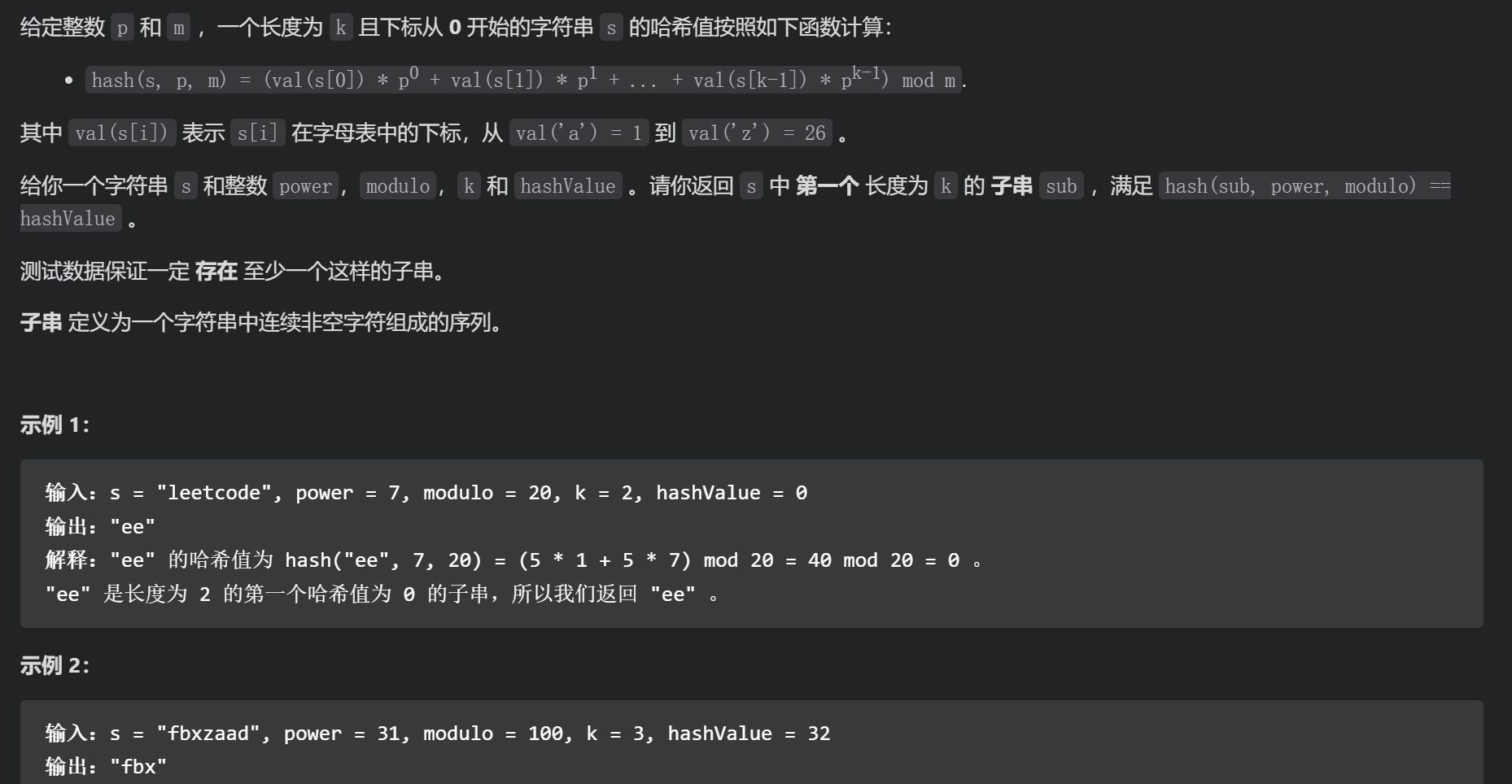
// 反向滑动窗口，下一个窗口的前k-1个字符的字符串哈希=这一个窗口的后k-1个字符的字符串哈希值*p
func subStrHash(s string, power int, modulo int, k int, hashValue int) string {
    pk_map := make(map[int]int) // p的n次幂：pk_map[i]: p^i % m
    pk_map[0] = 1 % modulo
    for i := 1; i < k; i++ {
        pk_map[i] = (pk_map[i-1] * power % modulo) % modulo
    }
    ans := 0
    tmp_hv := 0
    i := len(s) - 1
    for ; i >= len(s) - k ; i-- {
        tmp_hv = (tmp_hv * power + int(s[i])-int('a')+1)  % modulo
    }
    if tmp_hv == hashValue {
        ans = i + 1
    }
    for ; i >=  0; i-- {
        tmp_hv_k := ((int(s[i+k])-int('a') + 1) * pk_map[k-1] ) % modulo
        tmp_hv = (tmp_hv - tmp_hv_k + modulo ) % modulo
        tmp_hv = (tmp_hv * power + (int(s[i])-int('a')+1)) % modulo
        if tmp_hv == hashValue {
            ans = i
        }
    }
    return s[ans: ans+k]
}
// (a + b) % p = (a % p + b % p) % p 
// (a * b) % p = (a % p * b % p) % p 

快速幂

https://zhuanlan.zhihu.com/p/95902286

求解一个数的n次幂，如果只是将该数进行n此相乘，则需要进行n词运算，而使用快速幂则可以降低到logn。

例如求$5^{20}$，首先拆分为$5^{2*10}=5^{10} * 5^{10}$，只需要求$5^{10}$再乘上2，即一共11次运算；在此基础上再进行拆分为$5^5*5^5*5^5*5^5$，即一共9此运算，以此类推。

因此快速幂实际上是一种二分的思想，可以写出一个递归方程，对于$a^n$：

$a^n = \left \{ \begin{aligned} a^{n-1} \times a, & \space if \space n \space is \space odd \\ a^{\frac{n}{2}} \times a^{\frac{n}{2}}, & \space if \space n \space is \space even \space but \space not 0 \\ 1, & \space if \space n = 0 \end{aligned} \right .$

非递归快速幂：

int qpow(int a, int n){
    int ans = 1;
    while(n){
        if(n&1)        //如果n的当前末位为1
            ans *= a;  //ans乘上当前的a
        a *= a;        //a自乘
        n >>= 1;       //n往右移一位
    }
    return ans;
}